图
基本概念,图结构对元素的限定更少,因此它描述应用问题的能力棍儿更强。
一、术语:
G=(V;E),两个要素,V:顶点;存在对应关系就顶点相连,这些连边构成了图的第二个要素:边集。E:边的总数。彼此之间存在这种关系并且存在连边的任何两个点,我们成为彼此邻接关系。还有一个关系:关联(顶点与某条边的关系),注意区分邻接关系(顶点与顶点关系)。
V-V:邻接
V-E:关联
树也是图的特列,只是图更一般化。是否允许顶点与自己连接(为了简便暂时不考虑)。
无向边:点与点之间无方向。有向边:边有方向。相对应的称为无向图和有向图。有的边有向有的没有就称为混合图,我们主要讨论有向图。
如上图左图,我们说C->A->D->B(简单路径,没有重复节点)经过了一条长度为3的路径。
同样如上图右图,这里我们说,C->A->B->A->D(复杂路径或者一般路径,有重复顶点)。且路径起点和终点可以重合的(这种路径我们称为环路)。有向无换图(没有任何环路)。
经过所有的边一次且恰好一次的环路称为欧拉环路。
经过每个顶点一次且恰好一次,称为汉密尔顿环路
二、实现:
对图的接口和操作规范做一个定义:1
2
邻接矩阵与关联矩阵。
邻接矩阵:表示顶点之间的关系。如下图: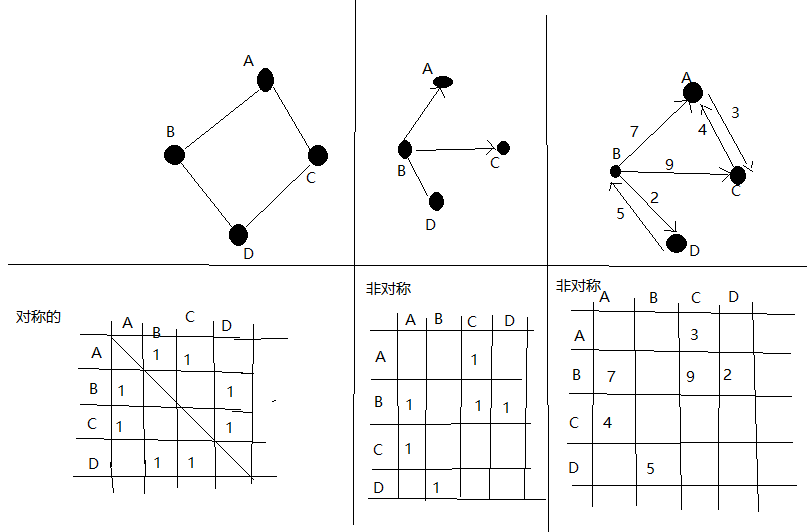
注意:在有向边中,矩阵表示的规则是:权重写在指向的那个顶点,比如A顶点指向B顶点,权重为3,那3就是写在矩阵中A的那边。当然,无向边是对称的。至于双向边,
